V programátorské praxi často intuitivně používáme některých operací, ale často si ani neuvědomujeme teoretický základ, ze kterého vycházejí. V nedávné době jsem se při programování potýkal s úpravou jednoho komplikovanějšího výrazu, který jsem chtěl nakonec upravit do jednoduššího tvaru. Při těchto úpravách jsem si uvědomil, že pro úpravu výrazů používám základní matematickou logiku – De Morganovy zákony. V následujícím článku si však projdeme pouze úpravu jednoduššího logického výrazu.
Nechť platí, že:
∪ - reprezentuje logickou operaci OR ∩ - reprezentuje logickou operaci AND
De Morganovy zákony nám říkají, že:
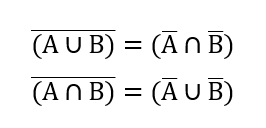
Reálná ukázka
Máme-li následující podmínku:
if (!(foo || bar)) {
// some code here
}
Můžeme ji upravit na:
if (!foo && !bar) {
// some code here
}Výše uvedená syntax je pouze pseudokód.
Pravdivostní tabulka:
| foo | bar | (!foo && !bar) | (!(foo || bar)) |
|---|---|---|---|
| 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 |
Zde vidíme, že obě výše uvedené podmínky jsou ekvivalentní – tj. pro stejné vstupní hodnoty se obě funkce chovají shodně.
Při implementaci konkrétních featur nebo při pozdějším refaktoringu budeme mít určitě mnoho možností pro upravování podmínek. Je třeba se ale míti na pozoru, jelikož jednodušší podmínka vždy neznamená její lepší čitelnost.
